在△ABC中，∠ACB=90°，∠ABC=30°，将△ABC绕顶点C顺时针旋转，旋转角为θ（0°＜θ＜180°），得到△A₁B₁C₁.
（1）如图1，当AB∥CB₁时，设A₁B₁与CB相交于点D.
证明：△A₁CD是等边三角形；
（2）如图2，连接A₁A、B₁B，设△ACA₁和△BCB₁的面积分别为和，
求证：： =1:3
（3）如图3，设AC中点为E，A₁B₁中点为P，AC=a，连接EP，当θ=_____°时，EP长度最大，最大值为_________.

如图，四边形ABCD是正方形，△ABE是等边三角形，M为对角线BD（不含B点）上任意一点，将BM绕点B逆时针旋转60°得到BN，连接EN、AM、CM.
（1）求证：△AMB≌△ENB；
（2）①当M点在何处时，AM＋CM的值最小；
         ②当M点在何处时，AM＋BM＋CM的值最小，并说明理由；
（3）当AM＋BM＋CM的最小值为时，求正方形的边长.

如图，△ABC中，∠ACB＝2∠B，BC=2AC.求证：∠A＝90°

如图是用火柴棍摆成边长分别是1、2、3根火柴棍时的正方形，当边长为n根火柴棍时，若摆出的正方形所用的火柴棍的根数为S，则S=________（用含n的代数式表示，n为正整数）
.

刘老师特制了4个同样的立方块，并将它们如图（a）放置，然后又（b）放置，则（b）中四个底面正方形中的点数之和是（     ）

有下列几何体：（1）圆柱；（2）正方体；（3）棱柱；（4）球；（5） 圆锥；（6）长方体．则这些几何体中截面可能是圆的有（     ）

将一正方形纸片按下列顺序折叠，然后将最后折叠的纸片沿虚线剪去上方的小三角形.将纸片展开，得到的图形是（     ）

如图，一个4×2的矩形可以用3种不同的方式分割成2或5或8个小正方形，那么一个5×3的矩形用不同的方式分割后，小正方形的个数可以是______.

用12个大小相同棱长为1的小正方体搭成的几何体如图所示，标有正确小正方体个数的俯视图和此几何体的表面积是（     ）

十八世纪瑞士数学家欧拉证明了简单多面体中顶点数（V）、面数（F）、棱数（E）之间存在的一个有趣的关系式，被称为欧拉公式．请你观察下列几种简单多面体模型，解答下列问题：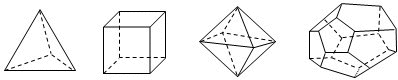
       四面体     长方体      正八面体     正十二面体
（1）根据上面多面体模型，完成表格中的空格：

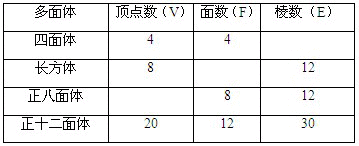
你发现顶点数（V）、面数（F）、棱数（E）之间存在的关系式是_______________．
（2）一个多面体的面数比顶点数大8，且有30条棱，则这个多面体的面数是____________．
（3）某个玻璃鉓品的外形是简单多面体，它的外表面是由三角形和八边形两种多边形拼接而成，且有24个顶点，每个顶点处都有3条棱，设该多面体外表三角形的个数为x个，八边形的个数为y个，求x+y值．