已知：如图，AB∥CD，∠1=135°，∠3=75°，求∠2的度数．为了求∠2的度数，某同学添加辅助线：延长BA交CE于点F．请你作出辅助线，并计算∠2的度数为(    )

• A. 45°
• B. 75°
• C. 30°
• D. 105°

（上接第5题）根据第5题添加的辅助线，可得∠HDC的度数为(    )

• A. 54°
• B. 44°
• C. 34°
• D. 134°

（上接第3题）根据第3题添加的辅助线，可得∠ACE的度数为(    )

• A. 130°
• B. 125°
• C. 135°
• D. 145°

已知：如图，在△ABC中，EF∥AD，∠EFD=80°，∠1=20°，∠2=50°，求∠DGC的度数．

解：如图，
                                 
∵∠DGC是△ADG的一个外角（外角的定义）
∴∠DGC=∠1+∠ADG（三角形的一个外角等于和它不相邻的两个内角的和）
∵∠1=20°（已知）
∴∠DGC=20°+30°
       =50°（等量代换）
横线处应填写的过程，顺序正确的是(    )
①∵EF∥AD（已知）
②∵∠EFD=80°（已知）
③∵∠2=50°（已知）
④∴∠ADC=80°（等量代换）
⑤∴∠ADC=∠EFD（两直线平行，同位角相等）
⑥∴∠ADF=180°-∠EFD=100°（两直线平行，同旁内角互补）
⑦∴∠ADG=∠ADC-∠2
         =80°-50°
         =30°（等式的性质）

• A. ①⑥③⑦
• B. ②④①⑤③⑦
• C. ①②④⑦
• D. ①⑤②④③⑦

已知：如图，AB∥DC，∠D=30°，BD平分∠ABC，求∠BCE的度数．

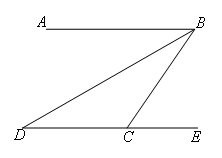
解：如图，
∵AB∥DC（已知）
∴∠ABD=∠D（两直线平行，内错角相等）
                                 
∵∠BCE是△BCD的一个外角（外角的定义）
∴∠BCE=∠D+∠CBD
       =30°+30°
       =60°（三角形的一个外角等于和它不相邻的两个内角的和）
横线处应填写的过程最恰当的是(    )

• A.
  ∵BD平分∠ABC（已知）
  ∴∠CBD=30°（角平分线的定义）
• B.
  ∵BD平分∠ABC（已知）
  ∴∠CBD=∠ABD（角平分线的定义）
  ∴∠CBD=∠D（等量代换）
  ∵∠D=30°（已知）
  ∴∠CBD=30°（等量代换）
• C.
  ∵BD平分∠ABC（已知）
  ∴∠ABC=2∠ABD（角平分线的定义）
  ∴∠ABC=2∠D（等量代换）
  ∵∠D=30°（已知）
  ∴∠ABC=60°（等式的性质）
• D.
  ∵BD平分∠ABC（已知）
  ∴∠ABC=60°（角平分线的定义）
  ∴∠DBC=30°（角平分线的定义）

已知：如图，CD平分∠ACB，∠1=30°，∠2=60°．
求证：∠B=∠ADE．

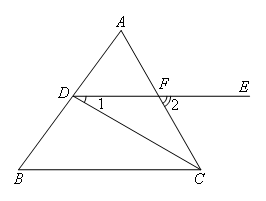
证明：如图，
∵∠2是△DFC的一个外角（外角的定义）
∴∠2=∠1+∠ACD（三角形的一个外角等于和它不相邻的两个内角的和）
∵∠1=30°，∠2=60°（已知）
∴∠ACD=∠2-∠1
       =60°-30°
       =30°（等式的性质）
                             
∴BC∥DE（内错角相等，两直线平行）
∴∠B=∠ADE（两直线平行，同位角相等）
横线处应填写的过程最恰当的是(    )

• A.
  ∴∠BCD=30°（角平分线的定义）
  ∴∠BCD=∠1（等量代换）
• B.
  ∵CD平分∠ACB（已知）
  ∴∠BCD=∠ACD（角平分线的定义）
  ∴∠BCD=30°（等量代换）
  ∴∠BCD=∠1（等量代换）
• C.
  ∴∠ACD=∠1（等量代换）
• D.
  ∵CD平分∠ACB（已知）
  ∴∠BCD=∠ACD（角平分线的定义）
  ∴∠2=∠BCF（等式的性质）

已知：如图，在四边形ABCD中，F是DC延长线上一点，AB∥CD，∠ECF=∠D，
∠CEF=∠F．
求证：∠1=∠2．

证明：如图，
∵AB∥CD（已知）
∴∠1=∠F（两直线平行，内错角相等）
∵∠ECF=∠D（已知）
∴BC∥AD（同位角相等，两直线平行）
                                   
横线处应填写的过程最恰当的是(    )

• A.
  ∴∠2=∠CEF（两直线平行，同位角相等）
  ∵∠CEF=∠F（已知）
  ∴∠1=∠2（等量代换）
• B.
  ∴∠2=∠BEA（两直线平行，内错角相等）
  ∵∠CEF=∠F（已知）
  ∴∠1=∠2（等量代换）
• C.
  ∴∠2=∠CEF（两直线平行，同位角相等）
  ∴∠1=∠2（等量代换）
• D.
  ∵∠CEF=∠F（已知）
  ∴∠2=∠F（两直线平行，同位角相等）
  ∴∠1=∠2（等量代换）

如图，AB∥CD，EF交AB于点G，交CD于点H，HP平分∠GHD，交AB于点P，∠AGE=50°，求∠PHD的度数．

解：如图，                                   
∴∠GHD=180°-∠GHC
       =180°-50°
       =130°（平角的定义）
∵PH平分∠GHD（已知）
∴∠PHD=∠GHD
       =×130°
       =65°（角平分线的定义）
横线处应填写的过程最恰当的是(    )

• A.
  ∵AB∥CD（已知）
  ∴∠GHC=∠AGE（两直线平行，同位角相等）
  ∴∠GHC=50°（等量代换）
• B.
  ∵AB∥CD（已知）
  ∴∠GHC=50°（两直线平行，同位角相等）
• C.
  ∵AB∥CD（已知）
  ∴∠GHC=∠AGE（同位角相等，两直线平行）
  ∵∠AGE=50°（已知）
  ∴∠GHC=50°（等量代换）
• D.
  ∵AB∥CD（已知）
  ∴∠GHC=∠AGE（两直线平行，同位角相等）
  ∵∠AGE=50°（已知）
  ∴∠GHC=50°（等量代换）

已知：如图，AB∥CD，∠A=∠D．
求证：AC∥DE．

证明：如图，
∵AB∥CD（已知）
∴∠A=∠ACD（两直线平行，内错角相等）
∵∠A=∠D（已知）
                                   
横线处应填写的过程最恰当的是(    )

• A.
  ∴∠ACD=∠D（等量代换）
  ∴AC∥DE（两直线平行，内错角相等）
• B.
  ∴∠ACD=∠D（等量代换）
  ∴AC∥DE（内错角相等，两直线平行）
• C.
  ∴AC∥DE（同位角相等，两直线平行）
• D.
  ∴∠ACD=∠D（等量代换）
  ∴AC∥DE（同位角相等，两直线平行）

已知：如图，将三角尺的直角顶点放在直尺的一边上，DF∥EG，∠1=30°，∠2=50°，求∠3的度数．

解：如图，
∵DF∥EG（已知）
∴∠AMD=∠2（两直线平行，同位角相等）
∵∠2=50°（已知）
∴∠AMD=50°（等量代换）
                                   
横线处应填写的过程最恰当的是(    )

• A.
  ∵∠AMD是△AMB的一个外角（外角的定义）
  ∴∠AMD=∠1+∠3（三角形的一个外角等于和它不相邻的两个内角的和）
  ∵∠1=30°（已知）
  ∴∠3=∠AMD-∠1
       =50°-30°
       =20°（等式的性质）
• B.
  ∵∠AMD是△AMB的一个外角（外角的定义）
  ∴∠3=∠AMD-∠1
       =50°-30°
       =20°（三角形的一个外角等于和它不相邻的两个内角的和）
• C.
  ∴∠3=∠AMD-∠1
       =50°-30°
       =20°（三角形的一个外角等于和它不相邻的两个内角的和）
• D.
  ∵∠AMD是△AMB的一个外角（外角的定义）
  ∴∠3=20°（三角形的一个外角等于和它不相邻的两个内角的和）