如图，点E为直线AB上一点，点F为直线CD上一点，点G为直线AB和CD内部的一点，根据几何原理下列作图正确的是(    )

• A. 连接EF，使EF⊥AB
• B. 连接EF，使EF⊥CD
• C. 过点G作直线MN∥AB
• D. 过点G作直线MN∥AB∥CD

根据下列要求作辅助线：①连接EF；②延长EO交CD于点H，其中符合要求的是(    )

• A.
• B.
• C.
• D.

已知：如图，AB∥EF．
求证：∠1+∠2-∠BCE=180°．

证明：如图，过点C作CG∥AB．

                             
∴∠3=180°-∠2（等式性质）
∵∠3=∠BCG-∠BCE（已知）
∴∠3=∠1-∠BCE（等量代换）
∴180°-∠2=∠1-∠BCE（等量代换）
∴∠1+∠2-∠BCE=180°（等式性质）
横线处应填写的过程恰当的是(    )

• A.
  ∴CG∥EF∥AB（平行于同一条直线的两条直线互相平行）
  ∴∠1=∠BCG（两直线平行，内错角相等）
    ∠2+∠3=180°（两直线平行，同旁内角互补）
• B.
  ∵AB∥EF（已知）
  ∴CG∥EF∥AB（平行于同一条直线的两条直线互相平行）
  ∴∠1=∠BCG（两直线平行，内错角相等）
    ∠2+∠3=180°（两直线平行，同旁内角互补）
• C.
  ∵AB∥EF（已知）
  ∴CG∥EF∥AB（平行于同一条直线的两条直线互相平行）
  ∴∠1=∠BCG（两直线平行，内错角相等）
• D.
  ∴CG∥EF∥AB（平行于同一条直线的两条直线互相平行）
  ∴∠1=∠3（两直线平行，内错角相等）
    ∠2+∠3=180°（两直线平行，同旁内角互补）

已知：如图，AB∥EF．
求证：∠1+∠2-∠BCE=180°．

证明：如图，

                             
∵∠3是△GCE的一个外角（外角的定义）
∴∠3=∠BCE+∠4（三角形的一个外角等于和它不相邻的两个内角的和）
∴∠1=∠BCE+∠4（等量代换）
∵∠4=180°-∠2（平角的定义）
∴∠1=∠BCE+180°-∠2（等量代换）
∴∠1+∠2-∠BCE=180°（等式性质）
横线处应填写的过程恰当的是(    )

• A.
  延长FE交BC于点G，
  ∵AB∥EF（已知）
  ∴∠1=∠3（两直线平行，内错角相等）
• B.
  延长FE到点G，
  ∵AB∥EF（已知）
  ∴∠1=∠3（两直线平行，内错角相等）
• C.
  延长FE交BC于点G，
  ∴∠1=∠3（两直线平行，内错角相等）
    ∠1=∠4（两直线平行，同位角相等）
• D.
  延长FE到点G，
  ∴∠1=∠3（两直线平行，内错角相等）

已知：如图，AB∥CD，AE∥DF，∠A=50°，∠C=25°，求∠F的度数．

解：如图，延长AE交CD于点G．

∵AB∥CD（已知）
                       
∵AE∥DF（已知）
∴∠F=∠2=105°（两直线平行，同位角相等）
以上空缺处所填正确的是(    )

• A.
  ∴∠1=∠A（两直线平行，内错角相等）
  ∵∠A=50°（已知）
  ∴∠1=50°（等量代换）
  ∵∠AEF是△ECG的一个外角（外角的定义）
  ∴∠AEF=∠1+∠C
         =50°+25°
         =75°（三角形的一个外角等于和它不相邻的两个内角的和）
• B.
  ∴∠1=∠A=50°（两直线平行，内错角相等）
  ∵∠C=25°（已知）
  ∴∠2=180°-∠1-∠C
       =180°-50°-25°
       =105°（三角形的内角和等于180°）
• C.
  ∴∠1=∠A（两直线平行，内错角相等）
  ∵∠A=50°（已知）
  ∴∠1=50°（等量代换）
  ∵∠C=25°（已知）
  ∴∠2=180°-∠1-∠C
       =180°-50°-25°
       =105°（三角形的内角和等于180°）
• D.
  ∴∠1=∠A=50°（两直线平行，内错角相等）
  ∴∠2=180°-∠1-∠C
       =180°-50°-25°
       =105°（三角形的内角和等于180°）

已知：如图，在四边形ABCD中，∠A=20°，∠B=40°，∠C=30°．求∠ADC的度数．

解：如图，延长AD交BC于点E．

∵∠1是△ABE的一个外角（外角的定义）
∴∠1=∠A+∠B（三角形的一个外角等于和它不相邻的两个内角的和）
                           
以上空缺处所填正确的是(    )

• A.
  ∵∠A=20°，∠B=40°（已知）
  ∴∠1=20°+40°
       =60°（等量代换）
  ∵∠C=30°（已知）
  ∴∠ADC=60°+30°
         =90°（等量代换）
• B.
  ∵∠A=20°，∠B=40°（已知）
  ∴∠1=20°+40°
       =60°（等量代换）
  ∵∠ADC=∠1+∠C（外角的定义）
  ∴∠ADC=60°+30°
         =90°（等量代换）
• C.
  ∵∠ADC=∠1+∠C（外角的定义）
  ∴∠ADC=∠A+∠B+∠C（三角形的一个外角等于和它不相邻的两个内角的和）
  ∴∠ADC=20°+40°+30°
         =90°（等量代换）
• D.
  ∵∠ADC是△CDE的一个外角（外角的定义）
  ∴∠ADC=∠1+∠C（三角形的一个外角等于和它不相邻的两个内角的和）
  ∴∠ADC=∠A+∠B+∠C（等量代换）
  ∵∠A=20°，∠B=40°，∠C=30°（已知）
  ∴∠ADC=20°+40°+30°
         =90°（等量代换）

已知：如图，AB∥CD．
求证：∠AEC=∠A+∠C．

证明：如图，

                           
∴∠A=∠1，∠2=∠C（两直线平行，内错角相等）
∴∠AEC=∠1+∠2
       =∠A+∠C（等式性质）
横线处应填写的过程最恰当的是(    )

• A.
  过点E作GH∥AB
  ∵AB∥CD（已知）
  ∴CD∥GH∥AB（平行于同一条直线的两条直线互相平行）
• B.
  过点E作GH∥AB∥CD
  ∴GH∥AB，CD∥AB，CD∥GH（平行于同一条直线的两条直线互相平行）
• C.
  过点E作GH∥AB
  ∴∠A=∠1（两直线平行，内错角相等）
• D.
  过点E作GH∥AB
  ∵AB∥CD（已知）
  ∴CD∥GH（平行于同一条直线的两条直线互相平行）
  ∴∠C=∠2（两直线平行，内错角相等）

已知：如图，CE平分∠ACD，点G是AB上一点，GF∥CE．若∠1=60°，∠2=20°，求∠BAC的度数．

解：如图，过点A作AH∥GF.

∵GF∥CE（已知）
∴CE∥AH∥GF（平行于同一条直线的两条直线互相平行）
                              
∵∠1=60°（已知）
∴∠4=60°（等量代换）
∴∠BAC=∠3+∠4
       =20°+60°
       =80°（等式性质）
横线处应填写的过程最恰当的是(    )

• A.
  ∴∠2=∠3=20°，∠4=∠5（两直线平行，内错角相等）
  ∵CE平分∠ACD（已知）
  ∴∠1=∠5=60°（角平分线的定义）
• B.
  ∴∠2=∠3=20°（两直线平行，内错角相等）
  ∵CE平分∠ACD（已知）
  ∴∠1=∠5（角平分线的定义）
  ∵∠4=∠5（已知）
  ∴∠4=∠1（等量代换）
• C.
  ∴∠2=∠3，∠4=∠5（两直线平行，内错角相等）
  ∵∠2=20°（已知）
  ∴∠3=20°（等量代换）
  ∵CE平分∠ACD（已知）
  ∴∠1=∠5=60°（角平分线的定义）
• D.
  ∴∠2=∠3，∠4=∠5（两直线平行，内错角相等）
  ∵∠2=20°（已知）
  ∴∠3=20°（等量代换）
  ∵CE平分∠ACD（已知）
  ∴∠1=∠5（角平分线的定义）
  ∴∠1=∠4（等量代换）

已知：如图，AB∥CD，E是AC上一点，∠B=30°，∠D=60°．求证：BE⊥ED.

证明：如图，

                              
∴∠B=∠1，∠D=∠2（两直线平行，内错角相等）
∵∠B=30°，∠D=60°（已知）
∴∠1=30°，∠2=60°（等量代换）
∴∠BED=∠1+∠2
       =30°+60°
       =90°（等式性质）
∴BE⊥ED（垂直的定义）
以上空缺处所填最恰当的是(    )

• A.
  过点E作EF∥AB∵AB∥CD
• B.
  过点E作EF∥AB
  ∵AB∥CD
  ∴CD∥EF∥AB（平行于同一条直线的两条直线互相平行）
• C.
  过点E作EF∥AB∥CD
• D.
  过点E作EF∥AB
  ∴CD∥EF∥AB（平行于同一条直线的两条直线互相平行）

已知：如图，AB∥CD，∠1=70°，∠2=60°，求∠B的度数．

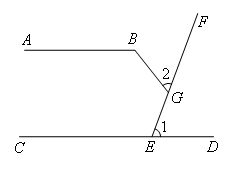
解：如图，过点G作GH∥AB，

                              
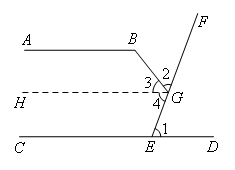
∴∠3=180°-∠2-∠4
       =180°-60°-70°
       =50°（平角的定义）
∴∠B=180°-∠3
       =180°-50°
       =130°（等式性质）
横线处应填写的过程最恰当的是(    )

• A.
  ∵AB∥CD（已知）
  ∴CD∥GH∥AB（平行于同一条直线的两条直线互相平行）
  ∴∠B+∠3=180°（两直线平行，同旁内角互补）
  ∵∠1=∠4，∠1=70°（已知）
  ∴∠4=70°（等量代换）
  ∵∠2=60°（已知）
• B.
  ∵AB∥CD（已知）
  ∴∠1=∠4（两直线平行，内错角相等）
    ∠B+∠3=180°（两直线平行，同旁内角互补）
  ∵∠1=70°（已知）
  ∴∠4=70°（等量代换）
• C.
  ∵AB∥CD（已知）
  ∴CD∥GH∥AB（平行于同一条直线的两条直线互相平行）
  ∴∠1=∠4=70°（两直线平行，内错角相等）
    ∠B+∠3=180°（两直线平行，同旁内角互补）
  ∵∠2=60°（已知）
• D.
  ∵AB∥CD（已知）
  ∴CD∥GH∥AB（平行于同一条直线的两条直线互相平行）
  ∴∠1=∠4（两直线平行，内错角相等）
    ∠B+∠3=180°（两直线平行，同旁内角互补）
  ∵∠1=70°（已知）
  ∴∠4=70°（等量代换）
  ∵∠2=60°（已知）