在菱形ABCD中,∠ABC=60°,E是对角线AC上一点.F是线段BC延长线上一点,且CF=AE.连接BE、EF.(1)若点E是线段AC的中点,如图1,则BE与EF的数量关系为BE       EF;

已知△ABC为等边三角形,点D为直线BC上的一动点(点D不与B、C重合),以AD为边作菱形ADEF,使∠DAF=60°,连接CF.(3)如图3,当点D在边CB的延长线上且其他条件不变时,AC、CF、CD之间的等量关系为()

已知△ABC为等边三角形,点D为直线BC上的一动点(点D不与B、C重合),以AD为边作菱形ADEF,使∠DAF=60°,连接CF.(2)如图2,当点D在边BC的延长线上且其他条件不变时,AC、CF、CD之间的等量关系为()

已知△ABC为等边三角形,点D为直线BC上的一动点(点D不与B、C重合),以AD为边作菱形ADEF,使∠DAF=60°,连接CF.(1)如图1,当点D在边BC上时,下列结论中:①BD=CF;②AC=CF+CD.正确的是()

已知,△ABC为等边三角形,点D为直线BC上一动点(点D不与B、C重合).以AD为边作菱形ADEF,使∠DAF=60°,连接CF.(3)如图3,当点D在边CB的延长线上且点A、F分别在直线BC的异侧时,其他条件不变,∠AFC、∠ACB、∠DAC之间的等量关系为()

已知,△ABC为等边三角形,点D为直线BC上一动点(点D不与B、C重合).以AD为边作菱形ADEF,使∠DAF=60°,连接CF.(2)如图2,当点D在边BC的延长线上时,其他条件不变,∠AFC、∠ACB、∠DAC之间的等量关系为(　)

已知,△ABC为等边三角形,点D为直线BC上一动点(点D不与B、C重合).以AD为边作菱形ADEF,使∠DAF=60°,连接CF.(1)如图1,当点D在边BC上时,下列结论:①∠ADB=∠AFC;②∠AFC=∠ACB+∠DAC.正确的是()

已知:正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,它的两边分别交CB,DC(或它们的延长线)于点M,N.(3)当∠MAN绕点A旋转到如图3的位置时,线段线段BM,DN和MN之间的数量关系为(　　)

已知:正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,它的两边分别交CB,DC(或它们的延长线)于点M,N.(2)当∠MAN绕点A旋转到BM≠DN时(如图2),线段BM,DN和MN之间有怎样的数量关系?写出猜想,并加以证明.

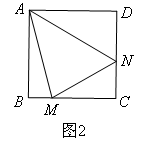
小王猜测线段BM,DN和MN之间的数量关系还为BM+DN=MN.理由如下:在∠MAN绕点A旋转到BM≠DN时,∠MAN的度数仍为45°,类比第一问,考虑仍用旋转的思想来做,(　),如图

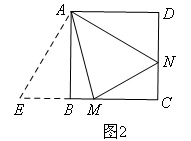
先证明△ABE≌△AND,用的三角形判定方法为(　),然后证明△EAM≌△NAM,用的三角形判定方法为(　),从而得出BM+DN=MN。括号内所填内容分别是(　　)

已知:正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,它的两边分别交CB,DC(或它们的延长线)于点M,N.(1)当∠MAN绕点A旋转到BM=DN时(如图1),证明BM+DN=MN

小王觉得∠MAN=45°,而∠BAD=90°,那么(　),两边的两个角的和是等于∠MAN的,所以考虑把这两个角拼在一起,考虑用旋转来转移角度,具体操作为:延长CB至点E,使得BE=DN,连接AE,如图:

这么一来构造出(　),从而∠DAN=∠BAE,那么∠EAM=∠EAB+∠BAM=∠DAN+∠BAM=45°,AE=AN,这样还可以得到DN+BM=BE+BM=EM,下面只需证明EM=MN即可,有(　)即可证明,从而得出BM+DN=MN.补充小王的思路,括号里填写顺序为(　　)①△EAM≌△NAM;②∠BAM+∠DAN=45°;③△ABE≌△AND;